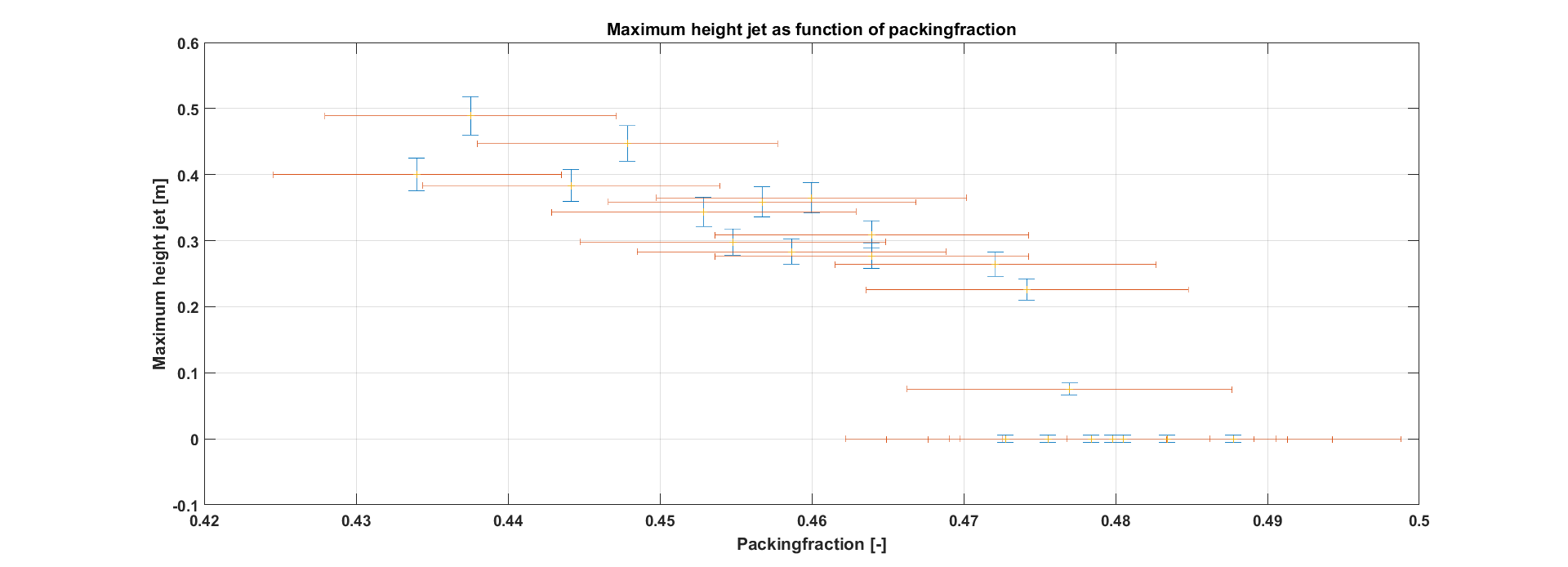
From the figure below, a critical value for the packing fraction at which a jet arises can be observed. The critical packing fraction for this specific impact velocity lies around 0.475 m/s. For a packing fraction lower than the critical packing fraction, the height of the jet is quasi linear. This relation is not surprising, since in a less dense sand bed, the ball can penetrate further in the sand and the volume of the imploding sand is larger. An explanation for this critical packing fraction might be that whereas for a very dense packing fraction the ball doesn’t enter the bed at all, for a packing fraction closer and closer to the critical packing fraction the ball enters the bed more and more, until, at the critical packing fraction, a cavity can be formed and a jet appears.
From the graph below, it can be concluded that there is not a clear relation observed between the impact velocity and the jet height. The jet height increases with the impact velocity, but for a certain velocity the jet height becomes constant. This behavior could be explained by the fact that the drag force acting on the ball in the bed is quadratic with the velocity (Katsuragi & Durian (2007)). So, the velocity must be four times as high to double the penetration depth. Since the height of the jet is proportional to the penetration depth, the jet height does not increase much at high velocities. Because of the error in the jet height, the little increase in the jet height might not be observed at high velocities.
